- El álgebra es una de las principales de la matemática que se ocupa de operaciones con y entre símbolos, representados generalmente por letras (variables o incógnitas) y coeficientes.
- Su nombre proviene del árabe "al-yabr" que significa "reintegración".
- Es la rama con mayor aplicación en la matemática, pues permite representar problemas formales de la vida cotidiana, como por ejemplo, las ecuaciones y las proporciones.
- El Álgebra Elemental, como su nombre lo indica, comprende preceptos más básicos de la materia, introduciendo en operaciones aritméticas una serie de símbolos que representan cantidades o relaciones desconocidas. Esto es fundamentalmente, el manejo de ecuaciones y de variables, coeficiente, índices o raíces.
- El Álgebra Abstracta, también conocida como Álgebra Moderna, representa un grado mayor de complejidad respecto a la elemental, ya que se dedica al estudio de las estructuras algebraicas o sistemas algebraicos, que son conjuntos de operaciones asociables a elementos de un grupo de patrón reconocible.
ORGANIZADOR GRÁFICO:
PRINCIPALES TEMAS

DIVISIÓN POLINÓMICA


PRODUCTOS NOTABLES
- Son productos que cumplen reglas fijas y cuyo resultado puede ser escrito por simple inspección, es decir verificar la multiplicación.
- Estas operaciones son fáciles de recordar sin necesidad de efectuar la multiplicación correspondiente.
A continuación, te presentamos los más usados:
PROBLEMAS DESARROLLADOS
- Fuente: MateMovil
FACTORIZACIÓN
- Factorización es el procedimiento que permite escribir como multiplicación una expresión algebraica.
- Los factores o divisores de una expresión algebraica, son los términos, ya sean números y/o letras, que multiplicados entre sí dan como producto la primera expresión.
- Así por ejemplo, si multiplicamos "a" por "a+b" podemos ver que:
- Entonces, los factores o divisores de esta expresión algebraica son "a" y "a+b".
MÉTODOS UTILIZADOS PARA FACTORIZAR UN POLINOMIO
- Primero debes saber que, no todos los polinomios se pueden factorizar, ya que, al igual que en los números primos que sólo son divisibles por ellos mismos y por 1.
- Por ejemplo, el polinomio ax + by + cz, no se puede factorizar ya que, solo es divisible por la unidad. Es decir, este polinomio no tiene un factor en común.
- Para poder factorizar una expresión algebraica es necesario que siempre exista al menos un factor en común de una expresión algebraica es el máximo común divisor (M.C.D.) de los términos que la componen.
PROBLEMAS DESARROLLADOS
- Fuente: Matemáticas Profe Alex
- Fuente: math2me
- Fuente: Mate
DIVISIÓN POLINÓMICA
- DIVISIÓN DE MONOMIOS:
(25x2) / (5x) =
- Dividir los coeficientes. 25: 5 = 5
- Dividir la parte literal (las letras que aparecen en los monomios).
- De esta modo: (25x2) / (5x)= 5x
- DIVISIÓN DE UN POLINOMIO POR UN MONOMIO: Se obtiene dividiendo cada término del polinomio por el monomio, obteniendo como resultado otro polinomio. Ejemplo:

- DIVISIÓN DE UN POLINOMIO POR UN MONOMIO:

De este modo, llamamos exacta a la división cuando R(x) es igual a 0. Para realizar la división debemos actuar del mismo modo que la división entera de números naturales. Ejemplo:
P(x) = 3x3 + 13x2 - 13x + 2 ; V(x) = 3x - 2
Realizar la siguiente operación: (3x3 + 13x2 - 13x + 2) : (3x - 2) =
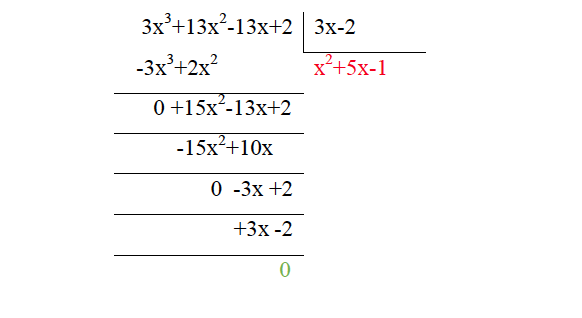
Así: C(x) = x2 - 5x + 1 y R(x) = 0
MÉTODOS PARA DIVIDIR POLINOMIO ENTRE POLINOMIO
MÉTODO DE RUFFINI
- Fuente: Abel Esteban Ortega Luna
MÉTODO DE HORNER
- Fuente: APRENDIENDO MATEMATICA
MÉTODO DEL TEOREMA DEL RESTO
- Fuente: Susi Profe
FUNCIONES
PROBLEMAS DESARROLLADOS
- Fuente: TodoSobresaliente
- Fuente: MateMovil
- Fuente: Matemáticas Profe Alex
- Fuente: MateMovil
- Fuente: julioprofe



No hay comentarios:
Publicar un comentario